Cantor Set
The Cantor Set was first published in 1883 by German mathematician Georg Cantor, who also created the basis of set theory. It is constructed as follows:
  1. take the interval [0, 1]
  2. remove the interval (1/3, 2/3), i.e. the middle part
  3. apply step 2) to the intervals left n times
The Cantor Set is constituted by those points not removed by the algorithm, e.g. 0, 1/3, 2/3, 1/9, and so on.

Author of the following procedures is Alain Schauber, Forbach, France. 


> with(plots):

> line := proc(a: list, b: list)
>    # substitute for Release 4 plotoptions/line in Release 3
>    local plotoptionen, n;
>    if nargs > 2 then
>       plotoptionen := seq(args[n], n=3 .. nargs)
>    else 
>       plotoptionen := NULL
>    fi;
>    plot([a, b], style=line, plotoptionen);
> end:

> cree_segment := (a,b,h) -> line([a,h],[b,h],color=red): 

> f1:=x->x/3: f2:=x->(x+2)/3:

> f := s -> s union map(f1, s) union map(f2, s): 

> sequence_de_segments := proc(l,h) 
> local accu, i;
> accu := NULL;
> for i to nops(l) by 2 do
> accu := accu,cree_segment(l[i], l[i+1], h) od;
> accu
> end:

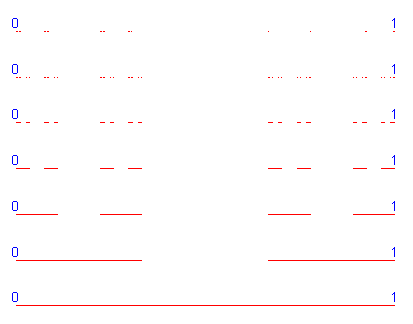
> Cantor := proc(n) local s, i;
> option remember;
> s := sequence_de_segments([0,1], 0);
> for i from 1 to n do
> s := s, sequence_de_segments(sort([op((f@@i)({0,1}))]), i/n)
> od;
> display({s}union{seq(textplot([[0,i/n, `0`], [1, i/n, `1`]], 
> align=ABOVE), i=0 .. n)}, color=blue,axes=NONE,thickness=0)
> end:

> Cantor(6);


last back next

Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mfrcant.htm