

yOne characteristic of fractals is that they are self-similar. An object is self-similar if its smaller parts always resemble the whole object. Affine maps determine how an object is rotated, moved, enlarged or shrinked. See Fractals for Windows by Tim Wegner, Bert Tyler, Mark Peterson and Pieter Brandenhorst for further details.
The following Maple procedures gave been written by Alain Schauber, Forbach, France, for Release 4.
> transforme_point := proc(t, p) > [t[1]*p[1]+t[2]*p[2]+t[5], t[3]*p[1]+t[4]*p[2]+t[6]] > end: > transforme_triangle := proc(t, triangle) > local i; > [seq(transforme_point(t, triangle[i]), i=1 .. 3)] > end: > IFS := proc(n, liste_de_transformations) > local i, j, k, s, sequence_de_triangles: > options `Copyright by Alain Schauber, 1996`; > sequence_de_triangles := [[0, 0], [1, 0], [0.5, 1]]; > for j to n do > s := NULL; > for i to nops(liste_de_transformations) do > s := s, > seq(transforme_triangle(liste_de_transformations[i], > op(k, [sequence_de_triangles])), > k=1 .. nops([sequence_de_triangles])) > od; > sequence_de_triangles := s > od; > plots[polygonplot]([sequence_de_triangles], axes=none, > color=black, scaling=constrained) > end: > tamis_de_Sierpinski:= > [[0.5,0,0,0.5,0,0],[0.5,0,0,0.5,0.5,0],[0.5,0,0,0.5,0.25,0.5]]: > arbre_de_Noel_double:= > [[0,-.5,.5,0,.5,0],[0,.5,-.5,0,.5,.5],[.5,0,0,.5,.25,.5]]: > labyrinthe_de_Sierpinski:= > [[evalf(1/3),0,0,evalf(1/3),evalf(1/3),evalf(2/3)], > [0,evalf(1/3),1,0,evalf(2/3),0], > [0,-evalf(1/3),1,0,evalf(1/3),0]]: > rameau:= > [[.387,.430,.430,-.387,.2560,.5220], > [.441,-.091,-.009,-.322,.4219,.5059], > [-.468,.020,-.113,.015,.4,.4]]: > cristal:= > [[.255,0,0,.255,.3726,.6714],[.255,0,0,.255,.1146,.2232], > [.255,0,0,.255,.6306,.2232],[.37,-.642,.642,.37,.6356,-.0061]]: > mecano:= > [[.382,0,0,.382,.3072,.619],[.382,0,0,.382,.6033,.4044], > [.382,0,0,.382,.0139,.4044],[.382,0,0,.382,.1253,.0595], > [.382,0,0,.382,.492,.0595]]: > feu:= > [[evalf(1/3),0,0,evalf(1/3),0,0], > [evalf(1/6),evalf(-sqrt(3)/6),evalf(sqrt(3)/6),evalf(1/6),evalf(1/3),0], > [evalf(-1/6),evalf(-sqrt(3)/6),evalf(sqrt(3)/6),evalf(-1/6), > evalf(2/3),0],[evalf(1/3),0,0,evalf(1/3),evalf(2/3),0]]: > arbre:= > [[.195,-.488,.344,.443,.4431,.2452],[.462,.414,-.252,.361,.2511,.5692], > [-.058,-.07,.453,-.11,.5976,.0969],[-.035,.07,-.469,-.022,.4884,.5069], > [-.637,0,0,.501,.8562,.2513]]: > maple := > [[0.29, 0.4, -0.4, 0.3, 0.28, 0.44], > [0.33, -0.34, 0.39, 0.4, 0.41, 0], > [0.42, 0, 0, 0.63, 0.29, 0.36], > [0.61, 0, 0, 0.61, 0.19, 0.23], > [0.01, 0, 0, 0.29, 0.5, 0.13]]: > tab15 := > [[-0.04, 0, -0.23, -0.65, -0.08, 0.26], > [0.61, 0, 0, 0.31, 0.07, 2.5], > [0.65, 0.29, -0.3, 0.48, 0.54, 0.39], > [0.64, -0.3, 0.16, 0.56, -0.56, 0.4]]: > koch:= > [[evalf(1/3), 0, 0, evalf(1/3), 0, 0], > [evalf(1/3), 0, 0, evalf(1/3), evalf(2/3),0], > [evalf(1/6),evalf(-sqrt(3)/6),evalf(sqrt(3)/6),evalf(1/6),evalf(1/3),0], > [-evalf(1/6),evalf(sqrt(3)/6),evalf(sqrt(3)/6),evalf(1/6),evalf(2/3),0]]: > tab21 := > [[0, 0, 0, 0.5, 0, 0], > [0.4, -0.4, 0.4, 0.4, 0, 0.2], > [0.4, 0.4, -0.4, 0.4, 0, 0.2]]: > IFS(8,tamis_de_Sierpinski);

> IFS(7,arbre_de_Noel_double);

> IFS(6,labyrinthe_de_Sierpinski);
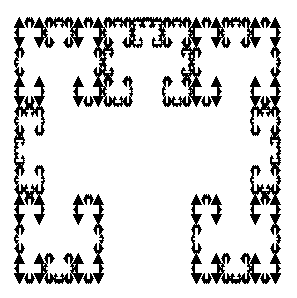
> IFS(7,rameau);
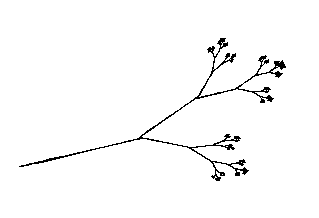
> IFS(5,cristal);

> IFS(4,mecano);

> IFS(5,feu);
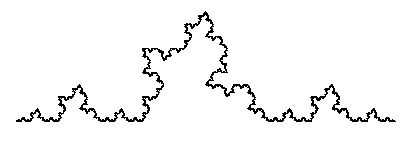
> IFS(5,arbre);

> IFS(5, maple);

> IFS(6, tab15);

> IFS(6, koch);

> IFS(8, tab21);
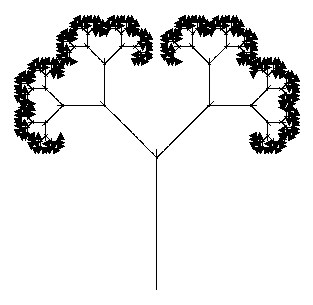
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mfrifs2.htm