Posted with permission of Robert J. Lopez. Copyright 1996 by Robert J. Lopez. All rights reserved.

This article has been published in MapleTech, Vol 4, NO. 3, 1997.

Tips for Maple Instructors

Robert J. Lopez
Department of Mathematics
Rose-Hulman Institute of Technology
Terre Haute, IN 47803

Release 4 MWS file of this article: tips3.mws (53,866 bytes).
R4 MWS files can be used in R5, as well.

In this, the third column of the series, we again illustrate some Maple V Release 4 functionality of significance in the classroom. In particular, we examine the role technology has in shaping pedagogy. Inescapably, the available technology dictates the operable pedagogy. In the pencil-and-paper world from which we are emerging, the lack of graphics and convenient numerical calculations, for example, imposed an analytical style on didactics, overshadowing experimentation and investigation.

In this issue's column, we consider two major topics. First, we examine the traditional approach to finding the recursion relation for a power series solution of a differential equation and compare that approach to one found in [1], the Maple V Flight Manual. Then, we explore the optimizing property of the Fourier series. Each of these items reflects how the available technology influences the pedagogy. In particular, each requires replacing infinite sums with finite sums in Maple.

In a third section, we look at three Maple functionalities that affect the student's view of Maple in the classroom. First, we consider an error Maple makes in the midst of a lesson on removable singularities. Then, we contrast plotting a curve defined vectorially in two and three dimensions. Finally, we examine some of the difficulties branches pose for both students and Maple in the computation of curvature of a circle.

I continue to hope this column becomes a forum where common problems can be identified and resolved, where useful hints and strategems can be found, and where pedagogical insights can be shared. Hence, I urge all readers who have their own experiences with Maple in instruction, successes and failures alike, to communicate with me by e-mail (mailto:r.lopez@rose-hulman.edu), fax(812-877-3198), or letter (Math Dept., Rose-Hulman Institute of Technology, Terre Haute, IN 47803). As much as possible, I would like this column to address real issues, from real classes. Only the column's readers can make that happen.

Series solutions of ODEs

> with(student):

> q := diff(y(x),x,x) + x^2*diff(y(x),x) + y(x) = 0;

Next, write a formal power series as the solution.

> Y :=sum(a[n]*x^n,n=0..infinity);

Substitute the series into the differential equation.

> q1 := eval(subs(y(x)=Y,q));

All powers of x submit to a combination of simplify and combine.

> map(simplify@combine,q1);

However, the indices on each separate series on the left of q1 must be shifted. We have to access and massage each such series separately. Unfortunately, this requires use of the "low-level" op command.

> for j from 1 to 3 do
> y.j := simplify(combine(op(j,lhs(q1))));
> od;

Shift indices so the power of x in the general term in each series is the same.

> y4 := changevar(n-2=k,y1,k);
> y5 := changevar(n+1=k,y2,k);
> y6 := changevar(n=k,y3,k);

Next, each sum must start at the same value of the index k. Here, we must have k = 1. In the first sum, the terms corresponding to k = -2 and -1 are zero. In the first and third sums, the terms corresponding to k = 0 must be extracted separately. In Maple, however, it is difficult to manipulate the indices in a mathematically meaningful way. We settle for an artifice permitted by the subs command.

> y4a := subs(-2=1,y4);
> y6a := subs(0=1,y6);

I suspect there would be a problem if "-2" or "-1" appeared in a context other than just the summation limits. Nonetheless, we are ready to combine the three transformed series.

> q2 := combine(y4a+y5+y6a);

We want a single coefficient of x^k. Hence,

> q3 := factor(q2);

The coeff command fails here, so we again resort to the low-level op command to access the summand of q3. (Fortunately, Release 5 will have a summand command to parallel the integrand command of the student package.)

> q4 := op(1,q3);

Now, coeff succeeds.

> q5 := coeff(q4,x^k);

Finally, we solve for a_k+2 in terms of a_k and a_k-1, resulting in the sought-for recursion relation.

> isolate(q5,a[k+2]);

Finally, with yet another artifice, we attend to the k = 0 terms in the series y4 and y6.

> value(subs(infinity=0,y4+y6)) = 0;

Rather than continue with the rest of the classical manipulations, we implement a device from [1] wherein a finite sum replaces the infinite series Y. The secret is to make the terms in the finite sum generic, and to span across the general term, xⁿ. Thus,

> Q := sum(a[k]*x^k,k=n-1..n+2);

Again, substitute into the differential equation.

> q6 := eval(subs(y(x)=Q,q));

When in doubt, simplify. This will tame all powers of x.

> q7 := simplify(q6);

Free of the baggage encumbering Sum, coeff now works. We map it onto both sides of the equation q7.

> q8 := map(coeff,q7,x^n);

Finally, solving for a_n+2, we get, in agreement with our earlier result,

> isolate(q8,a[n+2]);

Optimum property of Fourier series

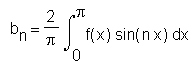
traditionally involves manipulating a formal infinite sum. In fact, these coefficients are those which minimize the integral

> q := Int((f(x) - Sum(s[n]*sin(n*x),n=1..infinity))^2,x=0..Pi);

In Maple, however, the differentiation

> diff(q,s[n]);

fails, since Maple does not "see" the general term s_n in the data structure it uses to represent the infinite sum. Thus, the traditional pedagogy used here must change if it is to be implemented in Maple. Typically, this change amounts to working with an explicit finite sum as in

> q1 := Int((f(x) - sum(s[n]*sin(n*x),n=1..3))^2,x=0..Pi);

Pay particular attention to the change from Sum to sum. Without that change the following differentiations fail.

> for k from 1 to 3 do
> eq.k := value(expand(diff(q1,s[k]),sin)) = 0;
> od;

Solving each equation for its single Fourier coefficient yields

> for k from 1 to 3 do
> isolate(eq.k, s[k]);
> od;

from which we generalize to the familiar result stated above.

Well, having to make this compromise left me feeling I had cheated my students. So, I thought I'd shift the same computations to a less familiar domain. I supposed a set of functions p0(x), p1(x), p2(x), ... with two properties:

1)

2)

I asked "Are these two properties enough to reproduce the minimization property of the Fourier series?"

To tell Maple that the functions p0(x), p1(x), p2(x) have these properties, define the following equations for Property (1).

> q01:=Int(p0(x)*p1(x),x=-1..1)=0;
> q02:=Int(p0(x)*p2(x),x=-1..1)=0;
> q12:=Int(p1(x)*p2(x),x=-1..1)=0;

Then define the following equations for Property (2).

> q00:=Int(p0(x)^2,x=-1..1)=2;
> q11:=Int(p1(x)^2,x=-1..1)=2/3;
> q22:=Int(p2(x)^2,x=-1..1)=2/5;

Now set up the same measure of performance as used for the Fourier series, namely, the integral of the square of the difference between the function f(x) and an approximating sum.

> Q := Int((f(x)-s0*p0(x)-s1*p1(x)-s2*p2(x))^2,x=-1..1);

Differentiate the measure of performance with respect to each of the three coefficients s0, s1, s2. Set the derivatives equal to zero to determine the values of the coefficients that minimize the measure of deviation Q.

> eq1 := diff(Q,s0) = 0;
> eq2 := diff(Q,s1) = 0;
> eq3 := diff(Q,s2) = 0;

Progress solving these equations depends on simplifying them. The parentheses need to be multiplied out, and any possible integrations done.

> eq4 := expand(eq1);
> eq5 := expand(eq2);
> eq6 := expand(eq3);

No integrations have been done because everything is symbolic. Maple knows only properties (1) and (2) apply, but can't apply them until told. Do this with a simplify command containing the equations that define Property (1) and Property (2).

> q0 := simplify(eq4,{q00,q11,q22,q01,q02,q12});
> q1 := simplify(eq5,{q00,q11,q22,q01,q02,q12});
> q2 := simplify(eq6,{q00,q11,q22,q01,q02,q12});

Solve each equation for the one coefficient it contains.

> isolate(q0,s0);
> isolate(q1,s1);
> isolate(q2,s2);

Generalize these definitions to a formula for the nth coefficient s_n.

Now, it was time to ask if such functions exist. Are there actually functions with properties (1) and (2)? My students didn't know, be we surely do, that the the functions p_n(x) are the Legendre polynomials, found in the orthopoly package.

> with(orthopoly);

A convenient way to access the first five Legendre polynomials uses the loop

> for k from 0 to 4 do
> p.k:=P(k,x);
> od;

Consider the function f(x) = sin(Pi x) on the interval [-1,1], and compute the coefficients s0, s1, s2, s3, s4 by the integral formulas derived above.

> for k from 0 to 4 do
> A[k]:=(k+1/2)*int(sin(Pi*x)*p.k,x=-1..1);
> od;

Form an approximating sum with these five coefficients. Note how the new add command lets us avoid the quotes needed by sum.

> s := add(A[n]*p.n,n=0..4);

Plot the approximation and the function f(x) on the same set of axes.

> plot([sin(Pi*x),s],x=-1..1,linestyle=[2,1],color=black);

Miscellaneous Maple observations

Evaluate-at

The function

> f := sin(3*x)/sin(4*x);

is easily found to have a removable discontinuity at x=0. Maple correctly evaluates

> q := Limit(f,x=0);

as

> value(q);

In an effort to show that there is indeed a discontinuity at x=0 we try

> subs(x=0,f);

a terribly erroneous result that steals all thunder from a lesson on removable discontinuities. Clearly, Maple has calculated and simplified that fraction to 1. The "error" is that Maple did not evaluate both numerator and denominator to 0. However, observe that if the expression f had been entered as a function, Maple's behavior would be different.

> F := unapply(f,x);

> F(0);
Error, (in F) division by zero

> g := piecewise(x<0,x, x<2,x^2);

> subs(x=1,g);

Substitution does not behave "mathematically" as "plug in and evaluate." However, if g is redefined as a function, evaluation occurs as expected.

> G := unapply(g,x);

> G(1);

Mike Monagan alerts me to a new paradigm coming in Release 5. Since subs is not the exact mathematical equivalent of substitution, a new eval command will support the notion of "plug in and evaluate at." Both of the examples above yield to this new functionality.

Plotting curves in vector form

The vector representation of a curve is a staple of a multivariable calculus course. Hence, representing a helix via the radius vector R = cos(t) i + sin(t) j + t k is most easily done in Maple with the syntax

> with(linalg):
> with(plots):
> R := vector([cos(t),sin(t),t]);

A plot of the helix is simply obtained via the syntax spacecurve(R, t = 0..4*Pi) but the analogous syntax for a plane curve will fail. For example, defining the plane curve

> r := vector([cos(t),sin(t)]);

and using the syntax plot(r, t = 0..2*Pi), fails to yield the expected circle since Maple treats the vector r as a list of two functions and plots a sine and a cosine curve. We are forced to treat the curve parametrically and address the components of the vector r. Hence, plotting a plane curve defined as a vector r requires plot([r[1], r[2], t = 0..2*Pi]). Such blurring of the roles of the vector and list data-structures in Maple requires students to remember syntactical particulars that add to the instructional overhead.

Curvature of a circle

Another staple in a multivariable calculus course is the notion of curvature of a plane curve. In fact, a standard shake-down of the definition of curvature is the verification that the curvature of a circle is a constant. This calculuation, however, requires deft handling of branches of the square root funtion.

We illustrate with a circle centered at the origin.

> q := x^2 + y^2 = a^2;

First, we obtain y(x) explicitly, and compute the curvature on the upper and lower semicircles separately.

> qq := solve(q,y):
> y1 := qq[1];
> y2 := qq[2];

Defining curvature as 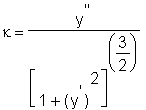we get

> kappa[1] := diff(y1,x,x)/(1+diff(y1,x)^2)^(3/2);
> kappa[2] := diff(y2,x,x)/(1+diff(y2,x)^2)^(3/2);

If we use simplification with respect to the side relation q, we obtain

> K1 := simplify(kappa[1],{q});
> K2 := simplify(kappa[2],{q});

from which an application of the radsimp command then yields

> radsimp(K1);
> radsimp(K2);

The difference in signs is significant. In contrast to newer caculus texts which define curvature with an absolute value, older calculus texts such as [2], define curvature so as to preserve information about concavity contained in the sign of y". Hence, on the upper semicircle, y(x) is concave downwards so y" is negative, whereas the opposite is true on the lower semicircle. Maple has yielded the correct results!

But we have violated Monagan's Prime Directive: Thou shalt not use radsimp under any circumstances! That command exists for backwards compatibility only. Thou shalt use simplify. It was luck that got us the correct answers. The weakness of radsimp, and the correct way to deal with the branches, are illustrated by the following computation based on implicit differentiation as implemented by the implicitdiff command.

> yx := implicitdiff(q,y,x);
> yxx := implicitdiff(q,y,x,x);

> kappa := yxx/(1+yx^2)^(3/2);

If we use the same combination of simplify and radsimp as before, we get

> radsimp(simplify(kappa,{q}));

Where exactly did we lose the sign information inherent in the curvature of the branches?

Clearly, simplifying [y²]^(3/2) to y³ is the culprit. It should be |y|³ so that [y/|y|]³ is either 1 or -1, depending on the branch y represents. The mathematically correct way (and the proper Maple way) to proceed is to simplify kappa with respect to the defining circle, then make assumptions on the signs of a, and y.

> q1 := simplify(kappa,{q});

> assume(a>0);
> interface(showassumed=0);

Returning to the computation at hand, on the upper semicircle, y(x) > 0, so

> assume(y>0);
> simplify(q1);

whereas on the lower semicircle, y(x) < 0, so

> assume(y<0);
> simplify(q1);

References

Biography

Author: Robert J. Lopez
Original file location: http://www.math.utsa.edu/mirrors/maple/mplrjl03.htm