

Category: Escape-time fractal
When I tried to program the Mandelbrot set myself the first time, I made the following mistake: instead of returning the ('original') point (x0, y0) that does not escape the radius of 2 about the orgin, the procedure returned the values of xn and yn which contain the values of the point (x0, y0) after its n-th iteration (here 25). (There is also the term orbit for the trajectory of a point being evaluated by the iteration formula zn+1 := zn2 + c).
> restart: with(plots): > alexerror:=proc(x, iter) > # written by Alexander F. Walz > # May 29, 1996 > # March 02, 1997 > local n, pts, xn, xnold, yn, y; > pts:=[0, 0]; > for y from 0 to 1.1 by 0.01 do > xn := x; > yn := y; > for n to iter while evalhf(xn^2+yn^2) < 4 do > xnold:=xn; > xn := evalhf(xn^2-yn^2+x); > yn := evalhf(2*xnold*yn+y) > od; > if n >= iter then pts := pts, [xn, yn], [xn, -yn] fi; > # as a variant try: > # "if n >= iter then pts := pts, [x, y] fi;" > # for the Mandelbrot set > od; > pts > end: > i:='i': > PLOT(seq(POINTS(alexerror(i/100)), i=-200 .. 70), SYMBOL(POINT));
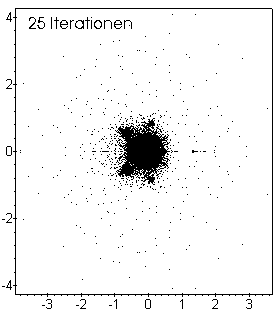
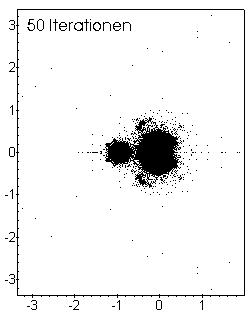
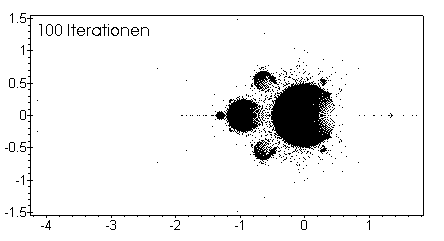

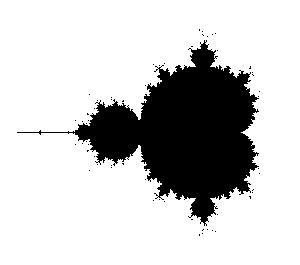

Merging of the Mandelbrot set and alexerror
after 100 iterations, both at the same scale.

MAPLE V FRACTALS AlexError #1.01 current as of May 23, 1999
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mfralex.htm