Maple V and Fractals: Julia Sets

Category: Escape-time Fractal

Julia sets are related to the Mandelbrot set in that the formula generating both is the same. The only difference is that for the Mandelbrot set the variable c is assigned the coordinates of the respective point [x, y] being iterated, so c changes for each point in the plane. In contrast, with Julia sets the variable c always remains the same for all the points in the plane:

Name	Iteration formula	Initialization of z	Initialization of c
Mandelbrot set	z_n+1 := z_n + c	z₀ := x + I*y	c = z₀ (variable)
Julia sets	z_n+1 := z_n + c	z₀ := x + I*y	c = a + I*b (fixed)

Thus, the Mandelbrot set can be seen as some sort of `catalogue` of Julia sets.


> restart; with(plots):

# Julia sets
#
# written by John Oprea, oprea@math.csuohio.edu

> julia := proc(c,x, y)
>    local z, m;
>    z := evalf(x+y*I);
>    for m from 0 to 30 while abs(z) < 3 do
>       z := z^2 + c
>    od;
>    m
> end:

> J := proc(d)
>    global phonyvar;
>    phonyvar := d;
>    (x, y) -> julia(phonyvar, x, y)
> end:

> plot3d(0, -2 .. 2, -1.3 ..1.3, style=patchnogrid, 
>    orientation=[-90,0], grid=[250, 250], 
>    scaling=constrained, color=J(-1.25));

Users of the Student Edition of both Release 3 and 4 have to decrease the value of the grid option to [70, 70] because of the limitation of the array size to 5120 elements.

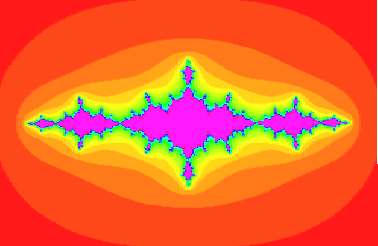
MAPLE V FRACTALS JULIA #1.1 current as of May 23, 1999
Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mfrjulia.htm