The sharetools package

The sharetools package has been designed to access and use the Maple V Release 5 Share Library in Maple 6 & 7.

The Share Library includes a lot of functions re mathematics, biology, chemistry, etc., that have been written by various Maple programmers. You can download it for free from

Install the Share Library in any location of your hard drive, preferably in a Maple subdirectory.

If you have got the original Maple V Release 5 distribution, install the Share Library from the second CD-ROM.

The current version is:

• sharetools v 1.0.0 for Maple 6 - December 16, 2001
• sharetools v 1.0.0 for Maple 7 - December 16, 2001

Functions:

• sharetools/readshare
  reads R5 Share Library functions.
• sharetools/loaded
  determines all names that have been readlib'ed.
• sharetools/restore
  restores functions that have been previously unprotected and overwritten by the readshare function.
• sharetools/findshare
  helps in finding the Share Library

Feedback

Availability

Netscape users should press and hold the SHIFT key when clicking on the UNIX TAR/GZIP links.

Version 1.0.0 for Maple 7 as of December 16, 2001 

• UNIX TAR/GZIP archive
• DOS PKZIP archive (compatible)

Version 1.0.0 for Maple 6 as of December 16, 2001 

• UNIX TAR/GZIP archive
• DOS PKZIP archive (compatible)

Demo

> restart:

> libname := libname, `e:/MapleV5/Share`;

> with(sharetools);

> readshare(partials);
Warning, help has been reassigned
Share Library: partials
Authors: Cheb-Terrab, Edgardo
Description: procedures for partial and functional derivatives

> D[2](L)(q(t),D(q)(t)):

> L(q(t),D(q)(t)):= cos(omega*diff(q(t),t)^(1/2))*q(t):

> usepdiff(%%);

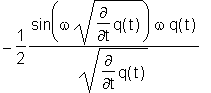
> readshare(ODE);
Share Library: ODE
Authors: Daniel Schwalbe
Description: package for solving ODE's numerically and plottingtheir solutions

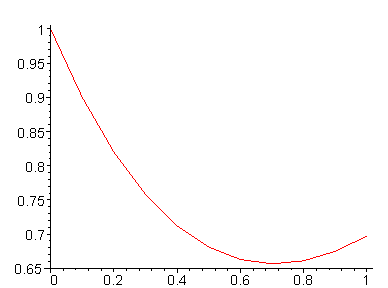
> eulerpts:=firsteuler((t,y)->t-y,[0,1],.1,10);

eulerpts := array(0 .. 10, [
        (0) = [0., 1.]
        (1) = [.1, .9]
        (2) = [.2, .82]
        (3) = [.3, .758]
        (4) = [.4, .7122]
        (5) = [.5, .68098]
        (6) = [.6, .662882]
        (7) = [.7, .6565938]
        (8) = [.8, .66093442]
        (9) = [.9, .674840978]
        (10) = [1.0, .6973568802]
        ])

> plot(makelist(eulerpts));

> readshare(FPS);
Share Library: FPS
Authors: Gruntz, Dominik
Description: FPS function attempts to find a formal power seriesexpansion for a function in terms of a formula for the coefficients

> FPS(sin(x), x=0);

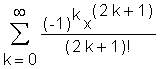
> readshare(elliptic);
Share Library: elliptic
Authors: Von York, Eric
Description: Determines the order of the group of points on a non-singular elliptic curve y^2 = x^3+A*x+B over a finite field Z mod p

> elliptic(47,1,1);

> readshare(turtle);
Share Library: turtle
Authors: Lozano, Eugenio Roanes
Description: package for supporting the Turtle graphics

> espiexag:=proc(n::integer) local l,i;
>     l:=2;
>     for i to n do
>           TurnRight(60);
>           l:=l+2;
>           Forwd(l)
>        od
>     end:

> ClearScreen();

> espiexag(60);

> FullScreen();

Author: Alexander F. Walz, alexander.f.walz@t-online.de
Original file location: http://www.math.utsa.edu/mirrors/maple/mplsharetools.htm